适用范围
蒂森克虏伯罗特艾德专门为其客户提供根据具体应用优化的使用期限。
术语“使用期限(utilization period)”在滚动轴承技术中被用作一个重要的比较参数,因为理论上的使用寿命在实际应用中通常不是一个绝对值,而是受许多影响因素决定的——根据 DIN ISO 281 和 DIN 26281——但这只是一个比较值,不是在所有情况下都必须达到的理论上的使用寿命,即使在大多数情况下,大多数轴承的使用寿命都会超过这个数值,而且在许多情况下会远远超过。
回转支承,对于回转运动或慢速旋转运动,通常只能在有限的范围内应用理论使用寿命的准则。通常,转动速度较低,这意味着平稳运行和精度不会受到磨损或个别点蚀的破坏性影响。
所以,对于承受回转运动或慢速旋转运动的回转支承,使用期限比理论上的使用寿命更具有决定性意义。当旋转阻力逐渐增加,或者磨损已经达到轴承功能不正常的程度,说明使用期限已经达到了。
回转支承在不同的运行条件下使用,要根据不同的运行方式,如可变的回转运动或者连续的旋转运动,不仅仅需要根据静态受力,还要根据受动态载荷影响的期望使用期限来选择回转支承。
在这种情况下,始终有必要区分设备的运行时间和回转支承的实际旋转或回转时间。必须考虑不同载荷的工作圈数和比例。另外,加载和不加载的回转角度也不能忽略,因为这是也是影响因素之一。
为了确定大致的使用期限,既可以使用静态边界荷载图,也可以使用“利用周期曲线”。对于系列25和系列23的异形轴承(profile bearing),只是配置了静态受力。
这些曲线是基于在满载下 30000 次转动的计算。它们可用于计算不同工作圈数下的utilization period或用于选择具有指定使用期限的轴承。
在曲线帮助下确定使用期限的做法,只适用于回转运动或慢速旋转运动的回转支承。这种做法不适用于,例如,
- 承受高径向力的轴承
- 承受高转速的轴承
- 必须具有高精度要求的轴承。
在这种情况下,需要由蒂森克虏伯罗特艾德根据工作圈数、对应的转速、时间占比进行计算。
| 符号 | 单位 | 说明 |
| G | U | Utilization period in rotations |
| G1,2,…i | U | Utilization period for duty cycles 1; 2; ...i |
| Fa | kN | Axial load |
| Mk | kNm | Tilting moment |
| Fa0 | kN | Axial load on the curve |
| Mk0 | kNm | Resulting tilting moment on the curve |
| Fa' | kN | "Read-off loading" calculated with fL |
| Mk' | kNm | "Read-off loading" calculated with fL |
| Fam | kN | Average axial load |
| Mkm | kNm | Average tilting moment |
| ED1,2,…i | % | Proportion of the operating time in % |
| p | Exponent | |
| Ball bearing p = 3 | ||
| Roller bearing p = 10/3 | ||
| fL | Ratio of the loads to the curve (load factor) [1] |
计算示例
示例1
回转支持的负载Fa=1250kN, Mk=2000kNm.
预计的使用期限是多少?
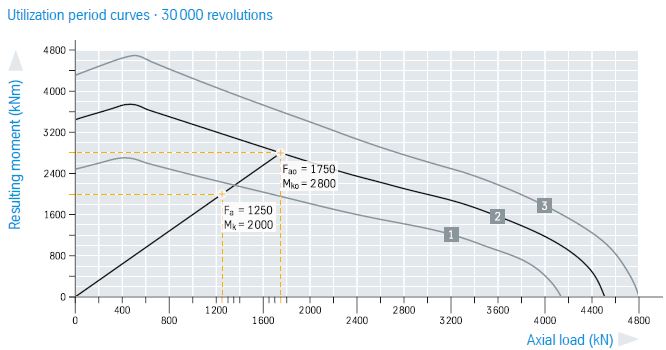
已知的载荷Fa和Mk被标记到曲线中。从图中原点通过指定载荷情况的直线与轴承的曲线相交,在本例中为轴承2的曲线,交点为(Fa0,Mk0)。
基于此,使用公式[1]和公式[2]来计算期望的使用期限:

使用时间可通过单位时间内的回转角度或旋转角度换算得出。
注意:如果可以定义多个不同的负载组合,则按照示例 2 计算预期使用期限。
示例2
还是对于轴承2,使用图中的载荷谱。
预计的使用期限是多少?
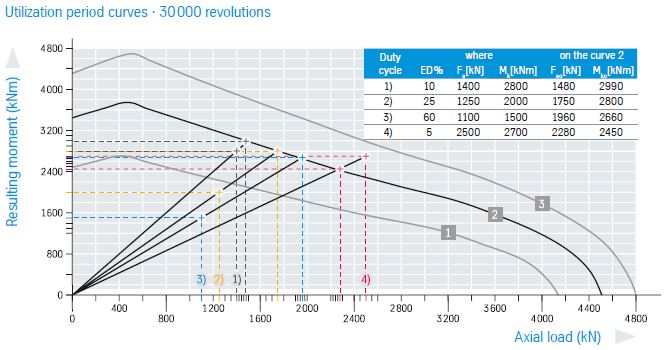
根据以上信息,针对每个工况计算使用期限G1,2,3,4。再用这些数值用公式 [3] 和各工况的的时间比例进行汇总,得出总使用期限。
